Select Medium
CLASS X PHYSICS CHAPTER 5
Refraction of Light
OVERVIEW
Refraction of light plays a crucial role in many daily applications, enabling us to see clearly through eyeglasses and contact lenses that correct our vision. It is essential in the design of cameras, microscopes, and telescopes, which rely on lenses to focus light and produce clear images. Additionally, refraction is responsible for natural phenomena such as rainbows and the twinkling of stars, enriching our visual experiences with the beauty of light.
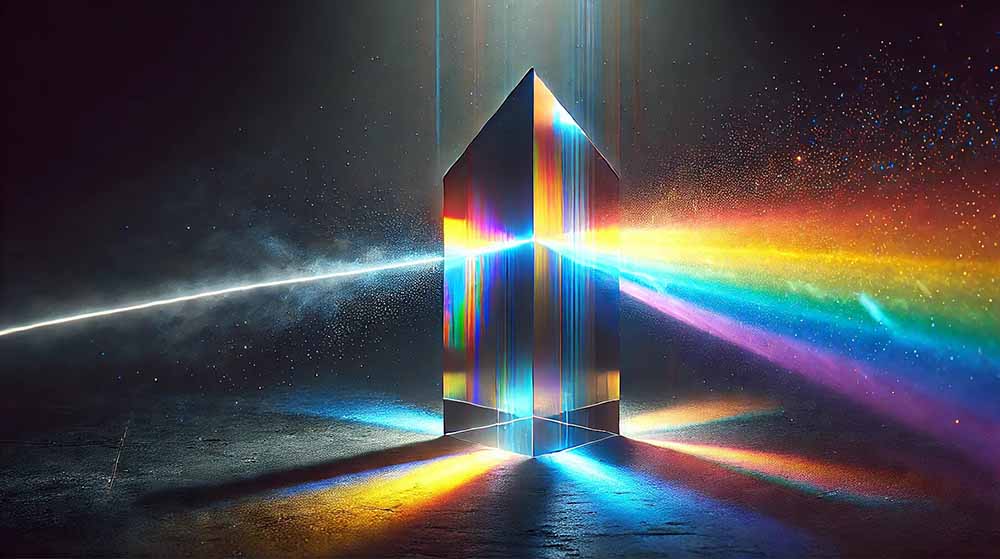
Speed of Light and Optical Density
The speed of light is a fundamental constant in physics, approximately 3 x 10^8 meters per second in a vacuum. Optical density refers to how much a medium can slow down light passing through it. The higher the optical density, the slower the speed of light in that medium. For example, light travels slower in water (refractive index 1.33) compared to air (refractive index 1.0003). This slowing down of light is due to the interaction between light waves and the particles within the medium, which absorb and re-emit the light. To remember, think of optical density as the “thickness” of a medium in terms of its effect on light speed. The relationship between the speed of light in a vacuum (c), the speed of light in the medium (v), and the refractive index (n) is given by n = c / v.
Refraction of Light
Refraction is the bending of light as it passes from one medium to another with different optical densities. This change in direction occurs because light changes speed when entering a new medium. For example, a straw in a glass of water appears bent at the water’s surface. The degree of bending depends on the angle of incidence and the refractive indices of the two media. To understand refraction better, draw diagrams showing light rays entering water at different angles and observe the bending. Remember, light slows down and bends towards the normal when entering a denser medium and speeds up, bending away from the normal, when entering a less dense medium.
Refraction in Different Media
The extent of refraction depends on the media involved. When light moves from air to water, glass, or diamond, the bending increases due to higher optical densities. Each medium has a specific refractive index, with air close to 1, water around 1.33, and diamond about 2.42. Real-world applications include lenses in glasses and cameras. A simple experiment to observe refraction involves placing a pencil in a glass of water and noting the apparent bending. To recall, visualize light as a car slowing down or speeding up when transitioning between different surfaces.
Laws of Refraction
The laws of refraction, also known as Snell’s Law, govern how light behaves when passing between media. The first law states that the incident ray, the refracted ray, and the normal at the point of incidence all lie in the same plane. The second law, Snell’s Law, is given by n1 sin θ1 = n2 sin θ2, where n1 and n2 are the refractive indices, and θ1 and θ2 are the angles of incidence and refraction, respectively. For better understanding, practice with different angles and media in a controlled setup. To remember, use mnemonic devices like “I Rarely Reflect Normal” to recall incident, refracted, and normal rays lying in the same plane.
Refraction Through Glass Prism
A glass prism disperses light into its constituent colors due to refraction. When white light enters a prism, different wavelengths bend by different amounts, causing dispersion. This separation of light into a spectrum can be seen in rainbows and prisms. The refractive index varies with wavelength, causing violet light to bend more than red light. Conducting a prism experiment in a dark room with a light source can visually demonstrate this concept. To remember, think of a prism as a tool for “unpacking” light, showing its colorful components.
Refractive Index
The refractive index of a medium is a measure of how much it slows down light compared to a vacuum. It is calculated as n = c / v, where c is the speed of light in a vacuum, and v is the speed in the medium. For instance, water has a refractive index of 1.33, meaning light travels 1.33 times slower in water than in a vacuum. Higher refractive indices indicate denser media. To reinforce this, compare the refractive indices of different materials and note how light bends more in media with higher refractive indices. Remembering specific refractive indices can be aided by creating a comparative chart of common substances.
Snell’s Law
Snell’s Law, given by n1 sin θ1 = n2 sin θ2, relates the angle of incidence and refraction to the refractive indices of the two media. This law helps predict the angle at which light will bend when moving between media. For example, if light enters water from air at an angle of 30°, Snell’s Law can determine the angle of refraction. Practice using Snell’s Law with different angles and media to build intuition. Visual aids like diagrams and interactive simulations can make the concept clearer. To remember, use real-world analogies like a swimmer changing speed when moving from water to land.
Relative Refractive Index
The relative refractive index is the ratio of the speed of light in one medium to that in another. It helps compare how light behaves when transitioning between specific pairs of media. For example, the relative refractive index of water to air is 1.33, indicating light travels 1.33 times slower in water. This concept is vital in designing optical instruments. To understand, experiment with light passing through different combinations of media. Creating a table comparing relative refractive indices of various pairs can aid in memorization.
Absolute Refractive Index
The absolute refractive index is the ratio of the speed of light in a vacuum to its speed in a given medium, represented as n = c / v. It indicates how much a medium slows down light. For instance, the absolute refractive index of diamond is 2.42. This concept is foundational in optics, affecting lens design and light propagation. To grasp this, compare the absolute refractive indices of several materials and observe their effects on light speed and direction. Visual tools like index cards with refractive indices can help in quick recall.
Calculating the Speed of Light
To calculate the speed of light in a medium, use the formula v = c / n. For example, if the refractive index of glass is 1.5 and the speed of light in a vacuum is 3 x 10^8 m/s, the speed in glass is (3 x 10^8 m/s) / 1.5 = 2 x 10^8 m/s. This calculation is crucial in various applications, including designing optical fibers and lenses. Practice with different refractive indices to become proficient. A tip for remembering is to keep the formula handy and use step-by-step calculations for accuracy.
Different Activities of Refraction
Refraction can be observed in numerous daily activities. Examples include the bending of light in a glass of water, the formation of rainbows, and the apparent bending of a straw in a drink. Conducting simple experiments like shining light through a prism or placing objects in water can illustrate refraction. Documenting observations in a journal can help reinforce the concepts. To remember, associate refraction with everyday experiences and natural phenomena, such as mirages and the sparkle of diamonds.
Total Internal Reflection
Total internal reflection occurs when light traveling from a denser to a less dense medium hits the boundary at an angle greater than the critical angle, causing it to reflect entirely within the denser medium. This principle is crucial in fiber optics and endoscopy. For example, light signals in optical fibers remain trapped due to total internal reflection, enabling high-speed data transmission. Experimenting with light passing through water or glass at various angles can demonstrate this effect. To remember, visualize total internal reflection as light “bouncing” entirely within the medium, unable to escape.
Critical Angle
The critical angle is the angle of incidence above which total internal reflection occurs. It depends on the refractive indices of the two media. For instance, the critical angle for light moving from water to air is about 48.6°. Calculating the critical angle using sin θc = n2 / n1, where n1 is the denser medium, reinforces the concept. Observing total internal reflection in practical setups, such as laser beams in water tanks, can provide a hands-on understanding. To remember, think of the critical angle as the “escape” threshold for light.
Optic Centre
The optic center of a lens is the point through which light rays pass without deviation. It is the geometric center of the lens and is crucial for understanding how lenses focus light. For instance, light passing through the optic center of a biconvex lens continues in a straight path. To understand, experiment with lenses and trace light paths through the optic center. Visual aids, such as diagrams showing light passing through different parts of the lens, can clarify the concept. To remember, consider the optic center as the “neutral” point in a lens.
Centre of Curvature
The center of curvature of a lens or mirror is the center of the sphere from which the lens or mirror is a segment. It lies on the principal axis and helps determine the curvature and focal length. For concave and convex mirrors, it is crucial in constructing ray diagrams. Practicing with ray diagrams to locate the center of curvature for various lenses and mirrors reinforces this concept. Using models or 3D software to visualize the center of curvature can aid understanding. To remember, associate the center of curvature with the origin of the lens’s curvature.
Principal Axis
The principal axis is the line passing through the centers of curvature of a lens or mirror and its optical center. It serves as a reference line for constructing ray diagrams and understanding image formation. For instance, light rays parallel to the principal axis converge at the focal point in a convex lens. Drawing and analyzing ray diagrams with respect to the principal axis helps in grasping this concept. To remember, visualize the principal axis as the “spine” of the optical system, providing structure and direction for light paths.
Principal Focus
The principal focus is the point where light rays parallel to the principal axis converge (for a convex lens) or appear to diverge from (for a concave lens). It is essential in understanding image formation and lens behavior. For example, a convex lens focuses sunlight to a point, demonstrating its principal focus. Conducting experiments with lenses to locate the principal focus can provide practical insights. To remember, think of the principal focus as the “target” where parallel light rays aim to meet.
Focal Length
The focal length is the distance between the optical center and the principal focus of a lens or mirror. It determines the converging or diverging power of the optical element. For example, a shorter focal length in a convex lens indicates a stronger converging ability. Calculating focal lengths using lens formulas and practicing with different lenses helps solidify this concept. Visual aids like focal length diagrams and hands-on experiments with varying lens types can enhance understanding. To remember, consider the focal length as the “reach” of the lens’s focusing ability.
Object Beyond 2F
When an object is placed beyond twice the focal length (2F) of a convex lens, the image formed is real, inverted, and smaller than the object. This principle is used in projectors and cameras. Practicing with ray diagrams to locate the image for objects at different positions relative to 2F reinforces this concept. Using lenses and measuring the distances can provide practical understanding. To remember, visualize the image shrinking and inverting as the object moves beyond 2F, simulating a projector’s function.
Images Formed by Convex and Concave Lens
Convex lenses form real, inverted images when the object is beyond the focal point and virtual, erect images when the object is within the focal point. Concave lenses always form virtual, erect, and smaller images. Understanding these principles through ray diagrams and practical experiments with lenses is crucial. For instance, a convex lens magnifying a close object demonstrates the formation of a virtual image. To remember, use the mnemonic “C-V-R-E” (Convex-Real when beyond, Erect when within) and “C-C-V-E” (Concave-Always Virtual Erect).
Power of a Lens
The power of a lens is the measure of its ability to converge or diverge light, defined as P = 1 / f, where f is the focal length in meters. It is measured in diopters (D). For example, a lens with a focal length of 0.5 meters has a power of 2D. Understanding the power of lenses helps in designing optical systems and prescribing corrective lenses. Calculating the power for different lenses and practicing conversions between focal length and power aids in comprehension. To remember, associate lens power with its focusing strength, like “optical muscles.”
Atmospheric Refraction
Atmospheric refraction is the bending of light as it passes through different layers of Earth’s atmosphere, each with varying densities. It explains phenomena such as the apparent shift in star positions and the flattening of the Sun at sunrise and sunset. Observing these effects in real life and understanding the principles behind them enhances comprehension. For instance, the twinkling of stars is due to atmospheric refraction. To remember, relate atmospheric refraction to the “bumpy ride” light takes through the layers of air.
Additional Tips for Remembering
Create Summary Charts: Develop comparative charts for refractive indices, focal lengths, and lens powers.
Visual Aids: Use diagrams and ray tracing to visualize concepts.
Hands-On Experiments: Conduct simple experiments with lenses, prisms, and water to observe refraction.
Analogies and Mnemonics: Create analogies and mnemonics to associate with complex terms.
Practical Applications: Relate each concept to real-life applications like cameras, eyeglasses, and fiber optics.
Consistent Review: Regularly revisit and review concepts to reinforce understanding.
Interactive Simulations: Utilize online simulations and apps to explore refraction phenomena dynamically.
Collaborative Learning: Discuss and explain concepts with peers to deepen understanding.
Key Points to Remember:
Speed of Light and Optical Density
- Speed of light in vacuum: ~3 x 10^8 m/s.
- Optical density affects how much light slows down in a medium.
- Higher optical density = slower light speed.
- Formula: n = c / v (n = refractive index, c = speed of light in vacuum, v = speed in medium).
- Example: Light travels slower in water (n = 1.33) than in air (n ≈ 1).
Refraction of Light
- Refraction is the bending of light as it passes between media of different densities.
- Light slows down and bends towards the normal in denser media.
- Example: A straw in water appears bent at the surface.
- Critical for understanding lenses, prisms, and everyday optical phenomena.
Laws of Refraction (Snell’s Law)
- Incident ray, refracted ray, and normal lie in the same plane.
- Snell’s Law: n1 sin(θ1) = n2 sin(θ2).
- Used to predict the angle of refraction.
- Essential for lens design and optical calculations.
Refractive Index
- Measure of how much light slows down in a medium.
- Calculated as n = c / v.
- Higher refractive index indicates a denser medium.
- Examples: Air (~1), water (1.33), diamond (2.42).
- Important for material identification and optical applications.
Total Internal Reflection and Critical Angle
- Occurs when light travels from a denser to a less dense medium at an angle greater than the critical angle.
- Critical angle: θc = sin^(-1)(n2 / n1).
- Used in fiber optics and other technologies.
- Light reflects entirely within the denser medium.
Focal Length and Power of a Lens
- Focal length (f): Distance from the lens to the focal point.
- Shorter focal length = stronger lens.
- Power (P) of a lens: P = 1/f (measured in diopters).
- Convex lenses converge light, concave lenses diverge light.
- Used in eyeglasses, cameras, microscopes.
Atmospheric Refraction
- Bending of light as it passes through Earth’s atmosphere.
- Causes apparent shifts in the position of celestial objects.
- Responsible for phenomena like the twinkling of stars.
- Critical for understanding optical illusions and astronomical observations.
Most Predicted Questions
The practice quizzes on SSLC A+ GENIUS feature the most predicted questions for SSLC exams, complete with detailed answers and tips. These interactive quizzes are designed to enhance your memory and performance, making exam preparation more effective and enjoyable.